Logaritma: Kunci Sukses Matematika

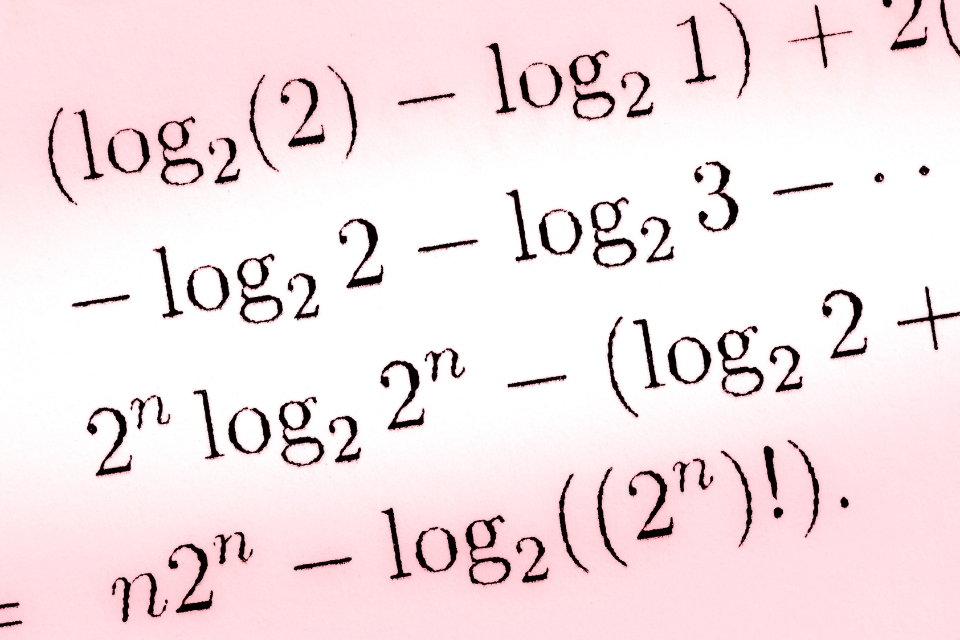
Logaritma merupakan salah satu materi penting dalam kurikulum matematika kelas 10 semester 1. Memahami konsep logaritma dengan baik akan membuka pintu pemahaman terhadap berbagai topik matematika lanjutan. Artikel ini akan membahas secara mendalam mengenai contoh soal logaritma kelas 10 semester 1 kurikulum 2013, lengkap dengan penjelasan langkah demi langkah.

Pendahuluan: Mengapa Logaritma Penting?

Logaritma pada dasarnya adalah kebalikan dari eksponen atau perpangkatan. Jika kita memiliki persamaan perpangkatan $a^b = c$, maka dalam bentuk logaritma dapat ditulis sebagai $log_a c = b$. Notasi ini dibaca "logaritma c dengan basis a sama dengan b".

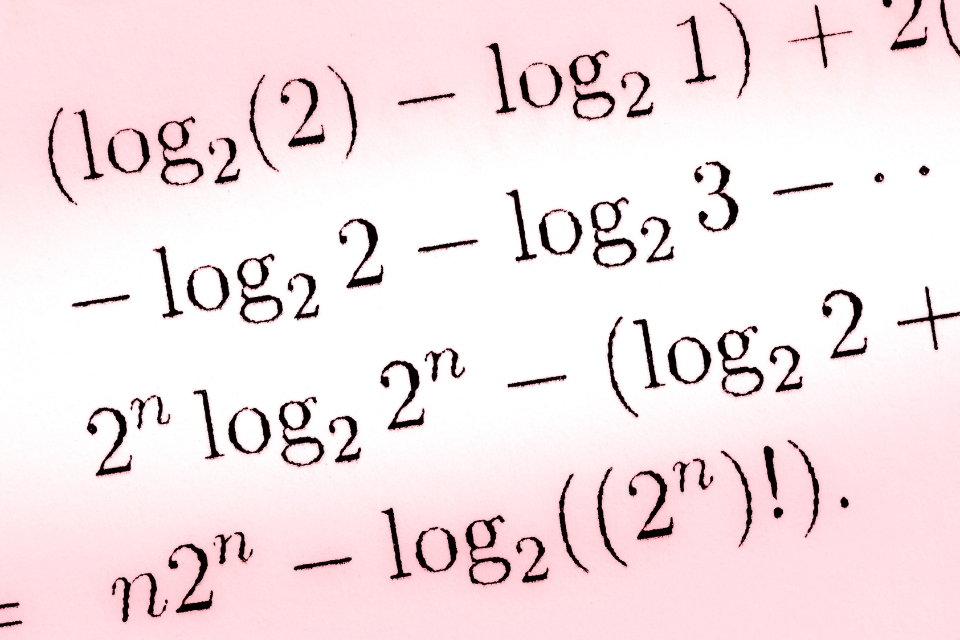
Mengapa logaritma menjadi penting? Logaritma memiliki banyak aplikasi dalam berbagai bidang, seperti:

Ilmu Pengetahuan Alam: Menghitung skala gempa bumi (skala Richter), tingkat keasaman (pH), intensitas suara (desibel), dan peluruhan radioaktif.
Teknologi Informasi: Mengukur kompleksitas algoritma komputasi.
Keuangan: Menghitung bunga majemuk dan pertumbuhan investasi.
Statistik: Menganalisis data dalam skala besar.

Dengan memahami logaritma, kita tidak hanya menguasai materi matematika, tetapi juga membuka wawasan tentang bagaimana matematika digunakan untuk memecahkan masalah di dunia nyata.

Bagian 1: Konsep Dasar Logaritma dan Sifat-sifatnya

Sebelum masuk ke contoh soal, mari kita ingat kembali definisi dan sifat-sifat dasar logaritma.

Definisi Logaritma:
Untuk $a > 0$, $a neq 1$, dan $c > 0$, maka $log_a c = b$ jika dan hanya jika $a^b = c$.

Sifat-sifat Logaritma yang Perlu Diingat:

$log_a 1 = 0$
Penjelasan: Berapapun basis logaritma (selama memenuhi syarat), jika numerusnya 1, maka hasilnya adalah 0. Karena $a^0 = 1$.
$log_a a = 1$
Penjelasan: Jika basis dan numerus sama, maka hasilnya adalah 1. Karena $a^1 = a$.
$log_a (M times N) = log_a M + log_a N$ (Sifat perkalian)
Penjelasan: Logaritma dari hasil perkalian dua bilangan adalah jumlah logaritma dari masing-masing bilangan.
$log_a (M / N) = log_a M – log_a N$ (Sifat pembagian)
Penjelasan: Logaritma dari hasil pembagian dua bilangan adalah selisih logaritma dari masing-masing bilangan.
$log_a (M^k) = k times log_a M$ (Sifat pangkat)
Penjelasan: Logaritma dari bilangan berpangkat adalah pangkatnya dikalikan dengan logaritma bilangan tersebut.
$log_a^n M = frac1n log_a M$ (Sifat basis berpangkat)
Penjelasan: Jika basis logaritma berpangkat, maka pangkat dari basis tersebut menjadi pembagi dari logaritma.
$log_a b times log_b c = log_a c$ (Sifat perubahan basis – bentuk sederhana)
Penjelasan: Ini adalah bentuk khusus dari sifat perubahan basis.
$log_a c = fraclog_b clog_b a$ (Sifat perubahan basis)
Penjelasan: Sifat ini memungkinkan kita untuk mengubah basis logaritma ke basis lain yang lebih mudah dihitung atau sesuai dengan soal. Biasanya digunakan basis 10 (logaritma biasa) atau basis $e$ (logaritma natural, dilambangkan ln).

Bagian 2: Contoh Soal dan Pembahasan Lengkap

Mari kita mulai dengan contoh soal yang umum ditemui di kelas 10 semester 1 kurikulum 2013.

Contoh Soal 1: Menghitung Nilai Logaritma Dasar

Hitunglah nilai dari:
a. $log_2 8$
b. $log_3 frac19$
c. $log5 1$
d. $log10 1000$

Pembahasan:

a. $log_2 8$
Kita mencari nilai $b$ sedemikian rupa sehingga $2^b = 8$.
Kita tahu bahwa $2^3 = 8$.
Jadi, $log_2 8 = 3$.

b. $log_3 frac19$
Kita mencari nilai $b$ sedemikian rupa sehingga $3^b = frac19$.
Kita tahu bahwa $9 = 3^2$.
Sehingga, $frac19 = frac13^2 = 3^-2$.
Jadi, $log_3 frac19 = -2$.

c. $log_5 1$
Menggunakan sifat $log_a 1 = 0$.
Jadi, $log_5 1 = 0$.

d. $log_10 1000$
Kita mencari nilai $b$ sedemikian rupa sehingga $10^b = 1000$.
Kita tahu bahwa $1000 = 10^3$.
Jadi, $log10 1000 = 3$.
(Perhatikan bahwa $log10$ seringkali ditulis sebagai ‘log’ saja tanpa menuliskan basisnya).

Contoh Soal 2: Menggunakan Sifat-sifat Logaritma

Sederhanakan atau hitunglah nilai dari ekspresi berikut:
a. $log_3 9 + log_3 27$
b. $log_2 48 – log_2 3$
c. $2 log_5 25$
d. $log_4 16^3$

Pembahasan:

a. $log_3 9 + log_3 27$
Menggunakan sifat perkalian: $log_a (M times N) = log_a M + log_a N$.
Kita bisa menghitungnya dengan dua cara:

Cara 1: Menghitung masing-masing logaritma terlebih dahulu.
$log_3 9 = 2$ (karena $3^2 = 9$)
$log_3 27 = 3$ (karena $3^3 = 27$)
Jadi, $2 + 3 = 5$.
Cara 2: Menggunakan sifat perkalian.
$log_3 9 + log_3 27 = log_3 (9 times 27) = log_3 243$.
Kita mencari nilai $b$ sedemikian rupa sehingga $3^b = 243$.
Kita tahu bahwa $3^5 = 243$.
Jadi, $log_3 243 = 5$.
Kedua cara memberikan hasil yang sama, yaitu 5.

b. $log_2 48 – log_2 3$
Menggunakan sifat pembagian: $log_a (M / N) = log_a M – log_a N$.
$log_2 48 – log_2 3 = log_2 left(frac483right) = log_2 16$.
Kita mencari nilai $b$ sedemikian rupa sehingga $2^b = 16$.
Kita tahu bahwa $2^4 = 16$.
Jadi, $log_2 16 = 4$.

c. $2 log_5 25$
Menggunakan sifat pangkat: $log_a (M^k) = k times log_a M$.
$2 log_5 25 = log_5 (25^2) = log_5 625$.
Kita mencari nilai $b$ sedemikian rupa sehingga $5^b = 625$.
Kita tahu bahwa $5^4 = 625$.
Jadi, $log_5 625 = 4$.

Atau, kita bisa menghitung $log_5 25$ terlebih dahulu:
$log_5 25 = 2$ (karena $5^2 = 25$)
Kemudian, $2 times log_5 25 = 2 times 2 = 4$.

d. $log_4 16^3$
Menggunakan sifat pangkat: $log_a (M^k) = k times log_a M$.
$log_4 16^3 = 3 times log_4 16$.
Kita tahu bahwa $log_4 16 = 2$ (karena $4^2 = 16$).
Jadi, $3 times 2 = 6$.

Contoh Soal 3: Menggunakan Sifat Perubahan Basis

Diketahui $log_3 2 = p$ dan $log_3 5 = q$. Tentukan nilai dari:
a. $log_3 10$
b. $log_3 50$
c. $log_9 10$

Pembahasan:

a. $log_3 10$
Kita bisa memecah 10 menjadi faktor-faktor yang berhubungan dengan basis 3 atau angka yang diketahui (2 dan 5).
$10 = 2 times 5$.
Menggunakan sifat perkalian: $log_3 10 = log_3 (2 times 5) = log_3 2 + log_3 5$.
Karena diketahui $log_3 2 = p$ dan $log_3 5 = q$.
Maka, $log_3 10 = p + q$.

b. $log_3 50$
Kita pecah 50 menjadi faktor-faktornya.
$50 = 2 times 25 = 2 times 5^2$.
Menggunakan sifat perkalian dan sifat pangkat:
$log_3 50 = log_3 (2 times 5^2) = log_3 2 + log_3 (5^2)$
$log_3 50 = log_3 2 + 2 log_3 5$
Substitusikan nilai yang diketahui:
$log_3 50 = p + 2q$.

c. $log_9 10$
Basis logaritma adalah 9, sedangkan informasi yang diberikan memiliki basis 3. Kita perlu menggunakan sifat perubahan basis.
Basis baru yang kita inginkan adalah 3.
Menggunakan sifat perubahan basis: $log_a c = fraclog_b clog_b a$.
Di sini, $a=9$, $c=10$, dan kita pilih $b=3$.
$log_9 10 = fraclog_3 10log_3 9$.

Kita sudah menghitung $log_3 10$ pada poin (a), yaitu $p+q$.
Kita juga perlu menghitung $log_3 9$.
$log_3 9 = 2$ (karena $3^2 = 9$).

Jadi, $log_9 10 = fracp+q2$.

Contoh Soal 4: Menggunakan Sifat Basis Berpangkat

Hitunglah nilai dari $log_16 8$.

Pembahasan:

Kita perlu mengubah basis 16 dan numerus 8 agar memiliki basis yang sama, yaitu 2.
$16 = 2^4$
$8 = 2^3$

Menggunakan sifat basis berpangkat: $log_a^n M = frac1n log_a M$.
Dan sifat pangkat: $log_a (M^k) = k times log_a M$.

$log16 8 = log2^4 2^3$

Kita bisa menerapkan sifat-sifat ini:
$log_2^4 2^3 = frac34 log_2 2$.
Karena $log2 2 = 1$.
Maka, $log16 8 = frac34 times 1 = frac34$.

Atau, kita bisa menggunakan sifat perubahan basis:
$log_16 8 = fraclog_2 8log_2 16$.
$log_2 8 = 3$ (karena $2^3 = 8$)
$log2 16 = 4$ (karena $2^4 = 16$)
Jadi, $log16 8 = frac34$.

Contoh Soal 5: Soal Cerita Sederhana

Suatu bakteri berkembang biak dengan membelah diri. Jumlah bakteri menjadi dua kali lipat setiap jam. Jika pada awal pengamatan terdapat 100 bakteri, berapa jumlah bakteri setelah 5 jam?

Pembahasan:

Ini adalah contoh penerapan logaritma (meskipun soalnya lebih sering diselesaikan langsung dengan eksponen, ini adalah dasar pemikirannya).

Jumlah bakteri setelah $t$ jam dapat dimodelkan dengan rumus:
$N(t) = N_0 times 2^t$
di mana:
$N(t)$ adalah jumlah bakteri setelah $t$ jam.
$N_0$ adalah jumlah bakteri awal.
$t$ adalah waktu dalam jam.

Dalam soal ini:
$N_0 = 100$
$t = 5$ jam

Jadi, jumlah bakteri setelah 5 jam adalah:
$N(5) = 100 times 2^5$
$N(5) = 100 times 32$
$N(5) = 3200$ bakteri.

Untuk melihat hubungannya dengan logaritma, jika ditanya "Berapa jam yang dibutuhkan agar jumlah bakteri menjadi 1600?", maka kita akan menggunakan logaritma:
$1600 = 100 times 2^t$
$16 = 2^t$
$log_2 16 = t$
$t = 4$ jam.

Contoh Soal 6: Soal Kombinasi Sifat

Tentukan nilai dari $fraclog_5 25 + log_5 125log_5 sqrt5$.

Pembahasan:

Mari kita hitung setiap bagian dari ekspresi:

Pembilang: $log_5 25 + log_5 125$
$log_5 25 = 2$ (karena $5^2 = 25$)
$log_5 125 = 3$ (karena $5^3 = 125$)
Jadi, pembilangnya adalah $2 + 3 = 5$.
Penyebut: $log_5 sqrt5$
Kita tahu bahwa $sqrt5 = 5^1/2$.
Menggunakan sifat pangkat: $log_a (M^k) = k times log_a M$.
$log_5 5^1/2 = frac12 log_5 5$.
Karena $log_5 5 = 1$.
Jadi, penyebutnya adalah $frac12 times 1 = frac12$.

Sekarang, kita gabungkan pembilang dan penyebut:
$frac5frac12$

Membagi dengan pecahan sama dengan mengalikan dengan kebalikannya:
$5 times frac21 = 10$.

Jadi, nilai dari $fraclog_5 25 + log_5 125log_5 sqrt5$ adalah 10.

Kesimpulan dan Tips Belajar Logaritma

Logaritma mungkin terasa menakutkan pada awalnya, tetapi dengan latihan yang konsisten dan pemahaman yang kuat terhadap sifat-sifatnya, Anda pasti akan menguasainya.

Tips untuk sukses belajar logaritma:

Pahami Definisi: Selalu ingat hubungan antara eksponen dan logaritma.
Hafalkan Sifat-sifatnya: Sifat-sifat logaritma adalah kunci untuk menyelesaikan berbagai soal. Tuliskan di kartu atau poster dan tinjau secara berkala.
Latihan Soal Beragam: Mulailah dari soal yang paling dasar, lalu tingkatkan kesulitannya secara bertahap.
Kerjakan Soal Secara Mandiri: Cobalah untuk menyelesaikan soal tanpa melihat kunci jawaban terlebih dahulu. Jika mentok, baru lihat petunjuk atau solusi.
Diskusikan dengan Teman: Belajar bersama teman dapat membantu Anda melihat sudut pandang yang berbeda dan memperjelas keraguan.
Manfaatkan Sumber Daya: Gunakan buku teks, catatan guru, dan sumber belajar online untuk memperkaya pemahaman Anda.

Dengan fokus dan dedikasi, Anda akan dapat menguasai materi logaritma dan siap menghadapi berbagai tantangan matematika di jenjang selanjutnya. Selamat belajar!